Teorema Enumerasi Polya #5: Permutasi adalah Pemetaan Bijektif ke Dirinya Sendiri

Permutasi sejatinya adalah suatu pemetaan bijektif dari suatu himpunan berhingga $X$ ke himpunan itu sendiri.

Kenapa bisa begitu?

Mari kita coba pahami dengan contoh. :)

 

Kembali pada contoh yang terdapat di artikel Teorema Enumerasi Polya #3: Permutasi Sebagai Pindah Letak. Kita memiliki tiga bola dengan warna berbeda, yaitu merah, kuning, dan hitam. Kita juga memiliki tiga mangkuk yang diberi nomor 1, 2, dan 3. 

Aturan yang berlaku adalah:

• Setiap satu mangkuk hanya dapat memuat satu bola, dan 
• Setiap bola harus berada di dalam mangkuk.

Jadi, dengan demikian setiap mangkuk akan memuat satu bola. Kita bisa menyebut bahwa bola berwarna $x$ berada dalam mangkuk nomor $y$.

 

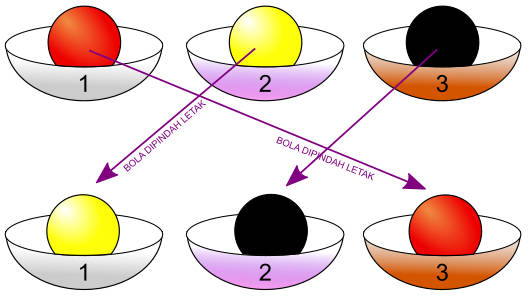
Dari ilustrasi di atas, permutasi dapat kita pandang sebagai sebagai ragam cara memindah letak bola pada mangkuk bernomor.

Hasil akhir pemindahan letak bola yang kita lakukan tersebut sama sekali tidak akan membuat mangkuk mana pun menjadi kosong. Oleh karenanya, pemindahan bola yang kita lakukan tersebut dapat kita pandang sebagai suatu pemetaan surjektif, yaitu setiap mangkuk dijamin tetap akan selalu berisi bola. 

Aturan bahwa satu mangkuk hanya dapat memuat satu bola menjamin bahwa pemindahan bola yang kita lakukan tersebut merupakan suatu pemetaan injektif. Karena pemindahan bola yang kita lakukan tersebut merupakan pemetaan surjektif sekaligus injektif, maka dapat disimpulkan bahwa pemetaan tersebut merupakan pemetaan bijektif.

 

Terakhir, jelas bahwa hasil akhir proses pemindahan letak bola tidak akan mengakibatkan jumlah bola menjadi berkurang maupun bertambah. Demikian pula dengan jumlah mangkuk bernomor.

Jumlah bola dan mangkuk tetap. Warna bola juga tetap alias tidak ada satu bola pun yang berubah warna. Demikian pula nomor dan warna mangkuk juga tidak ada yang berubah.

Oleh sebab itu, proses pemindahan letak bola merupakan suatu pemetaan dari suatu himpunan ke himpunan itu sendiri (dirinya sendiri).