Teorema Enumerasi Polya #3: Permutasi Sebagai Pindah Letak
Pada contoh di artikel Teorema Enumerasi Polya #2: Pengertian Permutasi, kita memandang permutasi sebagai cara urutan bola keluar dari dalam ember. Bola mana yang pertama keluar, bola mana yang kedua keluar, bola mana yang ketiga keluar, hingga bola mana yang terakhir keluar.
Nah, selain dari "sudut pandang" di atas, kita dapat melihat permutasi dari "sudut pandang" lain. Pada artikel ini kita kita akan memandang permutasi sebagai ragam cara memindah letak bola pada mangkuk bernomor.
Sudut pandang permutasi inilah yang kelak akan kita gunakan seterusnya pada pembahasan mengenai teorema enumerasi Polya.
Seperti apakah itu?
Mari simak contoh berikut.
Contoh
Mirip seperti contoh pada artikel Teorema Enumerasi Polya #2: Pengertian Permutasi, kita masih berkutat dengan himpunan $X$ yang elemennya adalah bola plastik berwarna merah, kuning, dan hitam.
$X = \{ \text{bola merah}, \text{bola kuning}, \text{bola hitam} \}$
Perbedaannya, kini kita juga memiliki 3 mangkuk yang masing-masing diberi nomor urut: 1, 2, dan 3. Bola-bola plastik berwarna kita letakkan di dalam mangkuk dengan aturan setiap mangkuk hanya dapat memuat satu bola.
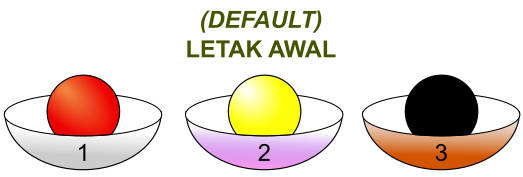
Sebagai letak awal (default), kita akan meletakkan:
- Bola merah di mangkuk nomor 1.
- Bola kuning di mangkuk nomor 2.
- Bola hitam di mangkuk nomor 3.
Ilustrasinya adalah seperti di bawah ini.
Berdasarkan letak awal bola-bola di atas, kita dapat memindahkan letak bola pada mangkuk.
Sebagai contoh, kita akan memindahkan letak bola dengan aturan berikut ini. Kita namakan aturan ini sebagai Aturan Pindah #1.
- Bola yang semula berada di mangkuk 1 dipindah ke mangkuk 3.
- Bola yang semula berada di mangkuk 2 dipindah ke mangkuk 1.
- Bola yang semula berada di mangkuk 3 dipindah ke mangkuk 2.
Ilustrasi di bawah memvisualisasikan perpindahan bola berdasarkan Aturan Pindah #1.
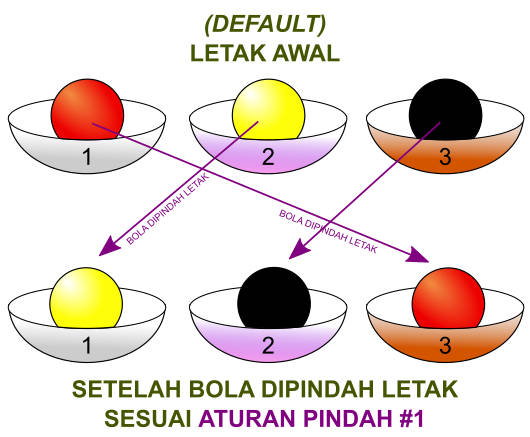
Diagram di bawah memvisualisasikan pemetaan perpindahan bola berdasarkan Aturan Pindah #1.
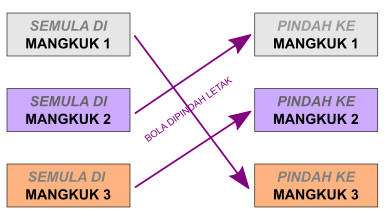
Jelas selain Aturan Pindah #1, kita juga dapat membuat aturan pindah yang lain. Katakanlah Aturan Pindah #2 semacam berikut.
- Bola yang semula berada di mangkuk 1 dipindah ke mangkuk 2.
- Bola yang semula berada di mangkuk 2 dipindah ke mangkuk 3.
- Bola yang semula berada di mangkuk 3 dipindah ke mangkuk 1.
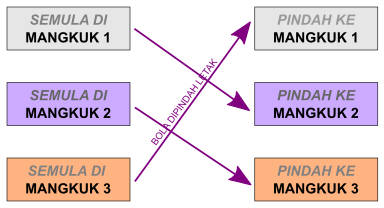
Diagram di bawah memvisualisasikan pemetaan perpindahan bola berdasarkan Aturan Pindah #2.
Ingat juga lho, bahwasanya ada yang disebut sebagai Aturan Pindah Identitas, yaitu semua bola pada mangkuk sama sekali tidak dipindah alias letaknya pada mangkuk tetap. ini dapat dinyatakan sebagai berikut.
- Bola yang semula berada di mangkuk 1 tetap berada di mangkuk 1.
- Bola yang semula berada di mangkuk 2 tetap berada di mangkuk 2.
- Bola yang semula berada di mangkuk 3 tetap berada di mangkuk 3.
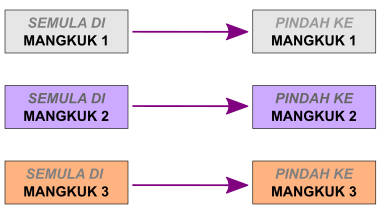
Diagram di bawah memvisualisasikan pemetaan perpindahan bola berdasarkan Aturan Pindah Identitas.
Sebagai penutup contoh.
Dari pembahasan di artikel Teorema Enumerasi Polya #2: Pengertian Permutasi, banyaknya Aturan Pindah yang dapat kita buat jelas adalah sebanyak $3! = 3 \times 2 \times 1 = 6$ aturan.
