Tunjukkan Relasi Ekuivalensi dan Partisinya (Contoh 1)

Yang namanya relasi ekuivalensi itu adalah topik wajib yang untuk pertama kalinya bakal disinggung saat belajar mata kuliah Pengantar Logika Matematika. Ya, kalau nggak paham tentang relasi ekuivalensi, nanti ya bakal bakal kerepotan sewaktu belajar mata kuliah Teori Himpunan atau Pengantar Struktur Aljabar. 

Yang jelas sih ya, relasi ekuivalensi pada suatu himpunan itu pasti bakal memunculkan yang namanya partisi. Kalau dibilang partisi itu ibaratnya partisi di hard disk komputer atau laptop. Misalnya, baru beli nih hard disk 500 GB. Nah, nanti kan umumnya bakal dipartisi itu hard disk, jadi semisal 250 GB untuk sistem (Drive C:), 100 GB untuk dokumen kerjaan (Drive D:), dan 150 GB untuk hiburan musik, video, dll (Drive E:). 

 

###

 

Oke! Kembali ke artikel ini!

Jadi, ceritanya, kali ini kita punya suatu relasi yang didefinisikan pada himpunan bilangan bulat ($\mathbb{Z} = \{ ..., -3, -2, -1, 0, 1, 2, 3, ... \}$). Kita akan menunjukkan bahwa relasi tersebut adalah suatu relasi ekuivalensi. Selain itu, kita juga akan menunjukkan seperti apa bentuk partisi yang tercipta di $\mathbb{Z}$ akibat relasi tersebut.

Nah! Buat para Pembaca yang mau ujian mata kuliah Pengantar Logika Matematika dan masih bingung perkara menjawab soal-soal relasi ekuivalensi, atau mungkin ingin memantapkan hati supaya lancar dan mulus menjawab soal-soal relasi ekuivalensi, silakan cermati isi artikel yang sebetulnya kurang bermanfaat ini, hahaha.

 

Soal

Didefinisikan relasi $\mathcal{R}$ pada himpunan bilangan bulat $\mathbb{Z}$ sebagai berikut.

$a \mathcal{R} b \iff (a-3)^2 + 2b = (b-3)^2 + 2a$, 
untuk setiap $a, b \in \mathbb{Z}$

1. Tunjukkan bahwa relasi $\mathcal{R}$ di atas merupakan relasi ekuivalensi pada $\mathbb{Z}$!
2. Tunjukkan partisi $\mathcal{P}$ pada $\mathbb{Z}$ yang terbentuk oleh relasi ekuivalensi $\mathcal{R}$ tersebut!

 

Dikerjakan

# 1. Menunjukkan bahwa $\mathcal{R}$ adalah relasi ekuivalensi

Oke!

Untuk menunjukkan bahwa $\mathcal{R}$ adalah relasi ekuivalensi, maka kita akan menunjukkan kebenaran tiga pernyataan di bawah ini.

 

# Sebelumnya...

Oh iya! 

Sebelum kita melangkah lebih jauh, alangkah baiknya kita perhatikan dulu sifat-sifat bilangan bulat berikut yang mana sudah jelas diketahui kebenarannya.

Selanjutnya, menggunakan sifat-sifat di atas, kita akan mendefinisikan ulang relasi $\mathcal{R}$ menjadi seperti berikut.

$a \mathcal{R} b \iff (a-3)^2 - 2a = (b-3)^2 - 2b$, 
untuk setiap $a, b \in \mathbb{Z}$

Definisi relasi $\mathcal{R}$ di atas, bisa kita sederhanakan menjadi seperti berikut.

$a \mathcal{R} b \iff a(a-8)  =  b(b-8)$, 
untuk setiap $a, b \in \mathbb{Z}$

 

#1.a Menunjukkan bahwa $\mathcal{R}$ adalah relasi refleksif.

Untuk menunjukkan bahwa $\mathcal{R}$ adalah relasi refleksif, maka kita akan menunjukkan bahwa berlaku $a \mathcal{R} a$ untuk sebarang $a \in \mathbb{Z}$.

Nah, ini jelas ya! Karena untuk sebarang $a \in \mathbb{Z}$ akan berlaku $a = a$ dan $a -8 = a - 8$, maka berdasarkan sifat yang ada di dalam kotak kuning di atas, maka kita akan punya persamaan berikut.

$a(a-8) = a(a-8)$

Jadi, karena ini berlaku untuk sebarang $a \in \mathbb{Z}$, maka berdasarkan definisi relasi $\mathcal{R}$, maka kita bisa menyatakan bahwa $a\mathcal{R}a$.

Jadi, dengan kata lain, kita bisa menyatakan bahwa $\mathcal{R}$ adalah relasi refleksif.

 

#1.b Menunjukkan bahwa $\mathcal{R}$ adalah relasi simetris.

Untuk menunjukkan bahwa $\mathcal{R}$ adalah relasi simetris, maka kita akan menunjukkan bahwa:

jika untuk setiap $a,b \in \mathbb{Z}$ yang memenuhi $a \mathcal{R} b$, maka akan berlaku juga $b \mathcal{R} a$.

Oke!

Misalkan, $a, b \in \mathbb{Z}$ adalah sebarang 2 bilangan bulat yang memenuhi $a \mathcal{R} b$. Dengan demikian, berdasarkan definisi relasi $\mathcal{R}$, maka kita akan punya persamaan $a(a-8) = b(b-8)$.

Nah ini!

Berdasarkan sifat yang ada di dalam kotak kuning di atas, maka pernyataan berikut akan berlaku benar.

$a(a-8) = b(b-8) \iff b(b-8) = a(a-8)$

Jadi, karena ini berlaku untuk sebarang $a,b \in \mathbb{Z}$ yang memenuhi $a \mathcal{R} b$, maka berdasarkan definisi relasi $\mathcal{R}$, maka kita bisa menyatakan bahwa $b\mathcal{R}a$.

Jadi, dengan kata lain, kita bisa menyatakan bahwa $\mathcal{R}$ adalah relasi simetris.

 

#1.c Menunjukkan bahwa $\mathcal{R}$ adalah relasi transitif.

Untuk menunjukkan bahwa $\mathcal{R}$ adalah relasi transitif, maka kita akan menunjukkan bahwa:

jika untuk setiap $a,b,c \in \mathbb{Z}$ yang memenuhi $a \mathcal{R} b$ dan $b \mathcal{R} c$, maka akan berlaku juga $a \mathcal{R} c$.

Oke!

Misalkan, $a, b, c \in \mathbb{Z}$ adalah sebarang 3 bilangan bulat yang memenuhi $a \mathcal{R} b$ dan $b \mathcal{R} c$. Dengan demikian, berdasarkan definisi relasi $\mathcal{R}$, maka kita akan punya persamaan $a(a-8) = b(b-8)$ dan $b(b-8) = c(c-8)$.

Nah ini!

Berdasarkan sifat yang ada di dalam kotak kuning di atas, maka pernyataan berikut akan berlaku benar.

$a(a-8) = b(b-8)$ dan $b(b-8) = c(c-8) \implies a(a-8) = c(c-8)$

Jadi, karena ini berlaku untuk sebarang $a,b, c \in \mathbb{Z}$ yang memenuhi $a \mathcal{R} b$ dan $b \mathcal{R} c$, maka berdasarkan definisi relasi $\mathcal{R}$, maka kita bisa menyatakan bahwa $a\mathcal{R}c$.

Jadi, dengan kata lain, kita bisa menyatakan bahwa $\mathcal{R}$ adalah relasi transitif.

 

## Kesimpulan.

Fiuh... menghela napas dulu ya!

Oke!

Berdasarkan penjabaran di atas, kita sudah menunjukkan kebenaran bahwasanya relasi $\mathcal{R}$ adalah relasi refleksif, simetris, dan juga transitif. Dengan demikian, kita bisa menyatakan bahwa relasi $\mathcal{R}$ adalah relasi ekuivalensi.

 

###

 

# 2. Menunjukkan partisi $\mathcal{P}$ pada $\mathbb{Z}$ yang terbentuk oleh relasi ekuivalensi $\mathcal{R}$ tersebut. 

Perhatikan!

Jika kita ambil sebarang bilangan bulat $x \in \mathbb{Z}$, maka $x - 8$ juga akan merupakan bilangan bulat. Iya toh!?

Nah ini! Perhatikan bahwa $x$ dan $x - 8$ adalah 2 bilangan bulat yang berbeda!

Iya nggak!? 

 

Nah, selanjutnya!

Perhatikan baik-baik definisi relasi $\mathcal{R}$ sebagaimana berikut.

$a \mathcal{R} b \iff a(a-8)  =  b(b-8)$, 
untuk setiap $a, b \in \mathbb{Z}$

 

Perhatikan bahwa $a(a-8)$ adalah bentuk faktorisasi polinomial. Nah, jika kita bentuk persamaan polinomial $a(a-8) = 0$, maka pembuat nol dari persamaan polinomial tersebut adalah $a = 0$ dan $a = 8$.

Dengan kata lain, akan berlaku:

• Untuk $a = 0$ $~\rightarrow~$ $a(a-8) = 0 \cdot (0 -8) = 0 \cdot -8 = 0$.
• Untuk $a = 8$ $~\rightarrow~$ $a(a-8) = 8 \cdot (8 -8) = 8 \cdot 0 = 0$.

Dengan demikian, kita bisa menyatakan bahwa $0 \mathcal{R} 8$. Dengan kata lain, bilangan $0$ dan $8$ termuat di dalam kelas ekuivalensi yang sama, sebut saja $\mathcal{P}_0$, yaitu $\mathcal{P}_0 = \{0, 8\}$.

  

Nah, bagaimana dengan kelas-kelas ekuivalensi yang lain, macamnya  $\mathcal{P}_1$, $\mathcal{P}_2$, $\mathcal{P}_3$, ..., $\mathcal{P}_{5 ~\text{milyar}}$, dan sebagainya?

 

Oh yeah! 

Sekedar informasi yang seharusnya kita sudah mengerti dengan baik.

Jika kita bentuk persamaan polinomial $f(x) = x(x-8) = x^2 - 8x$, maka grafik fungsi polinomial $f$ tersebut di bidang kartesius akan berbentuk parabola yang terbuka ke atas. Grafik fungsi polinomial $f$ tersebut memiliki titik minimum di $(4, -16)$ dan memotong sumbu $X$ di titik $(0,0)$ dan $(8,0)$.

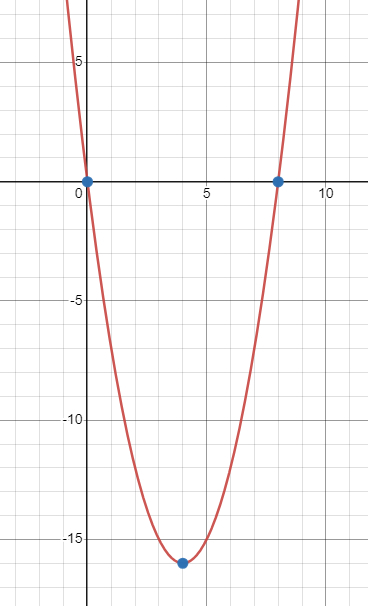
Perhatikan!

Jika fungsi polinomial $f(x) = x(x-8) = x^2 - 8x$ itu terdefinisi dengan baik untuk sebarang bilangan real $x$, maka fungsi polinomial $f(x)$ juga terdefinisi dengan baik untuk sebarang bilangan bulat $z$.

Iya nggak? 

Sebagaimana sifat bilangan bulat yang kita ketahui, jika $z$ adalah sebarang bilangan bulat, maka $f(z)$ juga akan merupakan bilangan bulat.

Iya kan?

Ingat bahwa kita dapat menghitung nilai $f(z)$ dengan menghitung nilai dari $z(z-8)$.

 

Oke! Selanjutnya, ini bakal menarik.

Kita ambil sebarang $z \in \mathbb{Z}$. Karena $z$ adalah bilangan bulat, maka sebagaimana yang sudah disinggung di atas, jelas bahwa nilai dari $f(z) = z(z-8)$ juga adalah bilangan bulat. 

 

Kemudian, jika kita bentuk polinomial $p$ dengan definisi $p(w) = w(w-8) - f(z)$, maka akan berakibat $z$ adalah salah satu pembuat nol polinomial $p$, yaitu $p(z) = 0$.

Iya nggak?

 

Akan tetapi, karena persamaan polinomial $p$ adalah polinomial berderajat 2, maka polinomial $p$ paling banyak memiliki 2 pembuat nol dan paling sedikit memiliki 1 pembuat nol.

Iya nggak?

 

Jadi, misalkan $p_{zero}$ adalah himpunan semua pembuat nol untuk polinomial $p$, yaitu $p_{zero} = \{ z \in \mathbb{Z} ~:~ p(z) = 0\}$, maka salah satu dari 2 kemungkinan berikut akan berlaku:

1. $p_{zero} = \{ z,~z' \}$ dengan $z \neq z'$, atau
2. $p_{zero} = \{ z \}$.

 

Nah, untuk mencari nilai $z$ dan mungkin juga $z'$, kita bisa memulai dengan menjabarkan polinomial $p$ terlebih dahulu sebagai berikut.

$p(w) = w(w-8) - f(z) = w^2 - 8w - f(z)$

Tentu saja, berdasarkan penjabaran di atas, kita bisa dengan mudah mencari bilangan bulat $w$ yang memenuhi persamaan $w^2 - 8w - f(z) = 0$ menggunakan Rumus ABC sebagai berikut.

Perhatikan bahwa nilai $a = 1$, $b = -8$ dan $c = -f(z)$.

$z, z' = \displaystyle \frac{-b \pm \sqrt{b^2 - 4ac} }{2a} = \frac{8 \pm \sqrt{64 + 4 \cdot f(z)} }{2}$

 

Ingat!

Karena $z$ adalah salah satu pembuat nol dari polinomial $p$, maka salah satu dari dua kemungkinan berikut akan berlaku.

$z =  \displaystyle \frac{8 + \sqrt{64 + 4 \cdot f(z)} }{2}$ atau $z =  \displaystyle \frac{8 - \sqrt{64 + 4 \cdot f(z)} }{2}$ 

 

## Jaminan Bahwa $z$ dan $z'$ adalah bilangan-bilangan bulat 

Seperti yang sudah disinggung di atas, diketahui bahwa $z$ adalah bilangan bulat. Kemudian, jika didefinisikan $f(z) = z (z - 8)$, maka jelas bahwa nilai dari $f(z)$ juga akan berupa bilangan bulat toh?

Selanjutnya, kita bentuk polinomial $p(w) = w(w-8) - f(z)$. Kita tahu bahwa $z$ adalah salah satu pembuat nol polinomial $p$, yaitu $p(z) = 0$.

Selanjutnya pula, dengan Rumus ABC, kita dapat menentukan pembuat nol yang lain (jika ada), yaitu $z'$, yang mana juga akan berlaku $p(z') = 0$.

Nah, keraguan muncul ketika kita tiba-tiba mempertanyakan bahwasanya apakah pembuat nol kedua (jika ada), yaitu $z'$ ini adalah bilangan bulat atau bukan.

 

Jawabannya jelas, bahwa $z'$ (jika ada) adalah bilangan bulat!

Kenapa bisa begitu?

Ingat! Misalkan $z$ dan $z'$ adalah pembuat nol polinomial $p$, maka kita bisa memfaktorkan polinomial $p$ sebagai berikut.

$p(w) = (w-z)(w-z')$

Karena $p(w) = w(w-8) - f(z) = w^2 - 8w - f(z)$ dan $f(z)$ adalah bilangan bulat, maka kita akan akan punya persamaan berikut.

$w^2 - 8w - f(z) = (w-z)(w-z')$

Dengan kata lain akan berlaku persamaan berikut.

$-f(z) = -z \cdot -z'$

Karena $f(z)$ dan $z$ adalah bilangan-bilangan bulat, maka supaya persamaan di atas berlaku benar, satu-satunya hal yang berlaku benar adalah $z'$ juga merupakan bilangan bulat.

Paham?

 

## Kesimpulan 

Berdasarkan penjabaran di atas, karena $\mathcal{R}$ adalah relasi ekuivalensi pada $\mathbb{Z}$, maka relasi $\mathcal{R}$ akan membagi $\mathbb{Z}$ ke dalam partisi-partisi $\mathcal{P}$.

Jika $z$ adalah sebarang bilangan bulat, maka partisi yang memuat $z$ dinotasikan $\mathcal{P}_z$ dengan definisi keanggotaan himpunan sebagai berikut.

$\mathcal{P}_z = \left\{ \displaystyle \frac{8 + \sqrt{64 + 4 \cdot z(z-8) } }{2},~ \displaystyle \frac{8 - \sqrt{64 + 4 \cdot z(z-8) } }{2} \right\}$

 

## Lebih Lanjut 

Karena grafik polinomial $f(x) = x(x-8)$ berbentuk parabola dan memiliki titik minimum di $(4, -16)$, maka partisi $\mathcal{P}_4$ adalah satu-satunya partisi yang memiliki satu anggota, yaitu $\mathcal{P}_4 = \{ 4 \}$.

Nggak percaya? Nih penjabarannya!

$\displaystyle \frac{8 + \sqrt{64 + 4 \cdot 4(4-8) } }{2} = \frac{8 + \sqrt{64 + (4 \cdot 4 \cdot -4) } }{2} = \frac{8 + \sqrt{64 - 64 } }{2} = \frac{8 + 0}{2} = 4$

dan

$\displaystyle \frac{8 - \sqrt{64 + 4 \cdot 4(4-8) } }{2} = \frac{8 - \sqrt{64 + (4 \cdot 4 \cdot -4) } }{2} = \frac{8 - \sqrt{64 - 64 } }{2} = \frac{8 - 0}{2} = 4$

 

## Dicocokkan 

Ayo kita tentukan $\mathcal{P}_0$, $\mathcal{P}_5$, dan $\mathcal{P}_{-37}$ dengan aturan di atas.

$\mathcal{P}_0 = \left\{ \displaystyle \frac{8 + \sqrt{64 + 4 \cdot 0(0-8) } }{2},~ \displaystyle \frac{8 - \sqrt{64 + 4 \cdot 0(0-8) } }{2} \right\}$

Karena:

$\displaystyle \frac{8 + \sqrt{64 + 4 \cdot 0(0-8) } }{2} = \frac{8 + \sqrt{64 + 0 } }{2} = \frac{8 + 8}{2} = 8$, dan

$\displaystyle \frac{8 - \sqrt{64 + 4 \cdot 0(0-8) } }{2} = \frac{8 - \sqrt{64 + 0 } }{2} = \frac{8 - 8}{2} = 0$, maka

$\mathcal{P}_0 = \left\{ 0, 8 \right\}$.

 

$\mathcal{P}_5 = \left\{ \displaystyle \frac{8 + \sqrt{64 + 4 \cdot 5(5-8) } }{2},~ \displaystyle \frac{8 - \sqrt{64 + 4 \cdot 5(5-8) } }{2} \right\}$

Karena:

$\displaystyle \frac{8 + \sqrt{64 + 4 \cdot 5(5-8) } }{2} = \frac{8 + \sqrt{64 - 60 } }{2} = \frac{8 + 2}{2} = 5$, dan

$\displaystyle \frac{8 - \sqrt{64 + 4 \cdot 5(5-8) } }{2} = \frac{8 - \sqrt{64 - 60 } }{2} = \frac{8 - 2}{2} = 3$, maka

$\mathcal{P}_5 = \left\{ 3, 5 \right\}$.

 

$\mathcal{P}_{-37} = \left\{ \displaystyle \frac{8 + \sqrt{64 + 4 \cdot (-37)(-37-8) } }{2},~ \displaystyle \frac{8 - \sqrt{64 + 4 \cdot (-37)(-37-8) } }{2} \right\}$

Karena:

$\displaystyle \frac{8 + \sqrt{64 + 4 \cdot (-37)(-37-8) } }{2} = \frac{8 + \sqrt{64 + 6.660 } }{2} = \frac{8 + 82}{2} = 45$, dan

$\displaystyle \frac{8 - \sqrt{64 + 4 \cdot (-37)(-37-8) } }{2} = \frac{8 - \sqrt{64 + 6.660 } }{2} = \frac{8 - 82}{2} = -37$, maka

$\mathcal{P}_{-37} = \left\{ -37, 45 \right\}$.