Pembuktian Limit Fungsi Kompleks Menggunakan Epsilon-Delta #1

Hadeh...

Mengerjakan soal pembuktian limit fungsi pakai $\epsilon$-$\delta$ jelas bikin kepala pusing dan mumet!

Apalagi kalau fungsinya adalah fungsi kompleks. Haduh! Makin tambah pusing deh!

Lha wong limit fungsi real saja sudah pusing kok. Ini malah fungsi kompleks. Pusingnya jadi berlipat-lipat ganda deh. :p

 

Eh, tapi yang namanya mahasiswa matematika ya. Mereka harus siap sedia grak! kalau urusan mengerjakan pembuktian limit fungsi pakai $\epsilon$-$\delta$ lho!

Sebabnya, pembuktian limit fungsi pakai $\epsilon$-$\delta$ itu adalah basic to the basic-nya ilmu analisis. Kalau nggak ada limit, mana ada yang namanya derivatif dan integral? Ya toh? :D

 

Oleh sebab itu, mari kita sekarang latihan mengerjakan pembuktian limit fungsi kompleks pakai $\epsilon$-$\delta$. Hitung-hitung persiapan buat ujian nanti. :D

Tenang saja! Bentuk fungsi kompleksnya nggak "keriting-keriting" amat kok. Ini nih.

 

Soal

Buktikan dengan konsep $\epsilon$-$\delta$ bahwa $\displaystyle \lim_{z \to i}{\frac{z}{z+i}=\frac{1}{2}}$!

 

Nggak susah kan bentuk fungsi kompleksnya?

Mirip-mirip dengan membuktikan bahwa $\displaystyle \lim_{x \to 1}{\frac{x}{x+1}=\frac{1}{2}}$ lah ya.

 

Tanpa berlama-lama, ayo kita kerjakan! :D

 

Pembahasan

Sebelum melangkah lebih jauh, ada baiknya kita mengenali dulu beberapa definisi dan sifat dalam semesta bilangan kompleks yang bakal kita pakai.

 

#Definisi-Definisi dan Sifat-Sifat yang Dipakai

Definisi pertama adalah tentang limit yang bentuk definisinya mirip dengan apa yang dijelaskan di mata kuliah Topologi.

 

Selanjutnya adalah definisi persekitaran di bilangan kompleks.

Sebagai ilustrasi dan contoh, di bawah ini adalah bentuk persekitaraan $V_6(-2+i) = \left\{ z \in \mathbb{C} ~:~ |z - (-2+i)| < 6 \right\}$.

 

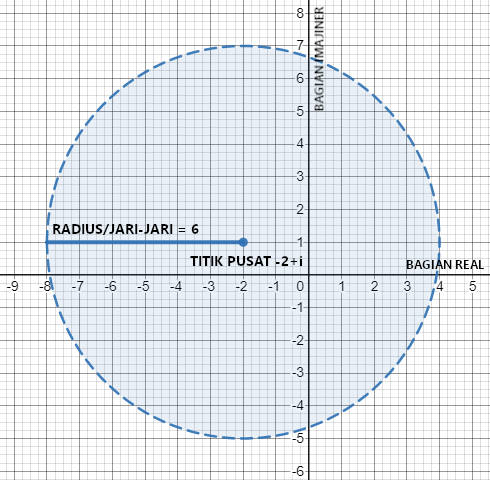
Kemudian ada sifat-sifat berikut.

 

#Langkah Pembuktian ke-1

Mengacu ke soal, kita bisa memisalkan $f(z) = \displaystyle \frac{z}{z+i}$, $L = \displaystyle \frac{1}{2}$, dan $c = i$. Dengan demikian, jika mengacu pada Definisi 1 maka kita akan memperoleh hasil sebagai berikut.
 

Ingat!

• $V_{\epsilon}(\frac{1}{2}) = \left\{ z \in \mathbb{C} ~:~ |z - \frac{1}{2}| < \epsilon \right\}$.
• $V_{\delta}(i) = \left\{ z \in \mathbb{C} ~:~ |z - i| < \delta \right\}$.

 

#Langkah Pembuktian ke-2

Oke, jadi kita diberikan sebarang persekitaran $V_{\epsilon}(\frac{1}{2})$.

Tugas kita adalah menentukan persekitaran $V_{\delta}(i)$ sedemikian sehingga untuk setiap $w \in V_{\delta}(i)$ akan berlaku $\displaystyle \frac{w}{w+i} \in V_{\epsilon}(\frac{1}{2})$.



Perhatikan bahwa yang dimaksud dengan menentukan persekitaran $V_{\delta(i)}$ itu tidak lain adalah menentukan $\delta$ yang sesuai.

Kemudian, berlaku $\displaystyle \frac{w}{w+i} \in V_{\epsilon}(\frac{1}{2})$ itu tidak lain adalah $\displaystyle \Bigg|\frac{w}{w+i} - \frac{1}{2}\Bigg| < \epsilon$.

Berdasarkan Sifat 2 dan Sifat 3, pertidaksamaan $\displaystyle \Bigg|\frac{w}{w+i} - \frac{1}{2}\Bigg| < \epsilon$ ekuivalen dengan  $\displaystyle \frac{\big|w-i\big|}{2\;\big|w+i\big|} < \epsilon$.

 

#Langkah Pembuktian ke-3

Hmmm... hmmm... hmmm... kira-kira nilai $\delta$ apa ya yang sesuai?

 

Hmmm... hmmm... hmmm...

 

Bagaimana kalau dipilih $\displaystyle \delta = \frac{1}{3}$?

Dengan demikian, selanjutnya kita akan menyelidiki persekitaran $V_{\frac{1}{3}}(i)$.

 

Di sini mungkin kalian akan bertanya, "Kenapa yang dipilih $\delta = \displaystyle \frac{1}{3}$?"

 

Jawabannya, "Karena sewaktu mengerjakan soal ini, aku sedang suka mendengarkan lagu 1/3 no Junjou na Kanjou yang menjadi ending song-nya anime Rurouni Kenshin."

"Kowareru hodo aishite mo
Sanbun no ichi mo tsutawaranai
Junjō na kanjō wa karamawari
I love you sae ienai de iru
My heart..."      

 

Huh....

Sangat tidak bermutu sekali jawaban di atas itu. :D

 

Sebetulnya, kita bebas menyelidiki persekitaran $V_{\delta}(i)$ untuk nilai $\delta$ berapapun asalkan kita mengusahakan agar nilai $\delta$ sekecil mungkin, seperti $\displaystyle \frac{1}{2}, \frac{1}{10}, \frac{1}{100}$, dan sebagainya.

 

#Langkah Pembuktian ke-4

Nah, ayo kita selidiki persekitaran $V_{\frac{1}{3}}(i)$!

Kita mulai dengan menjabarkan apa itu $V_{\frac{1}{3}}(i)$.

$V_{\frac{1}{3}}(i) = \left\{ z \in \mathbb{C} ~:~ |z - i| < \displaystyle \frac{1}{3} \right\}$

Jangan pernah lupa! Persekitaran pada bidang kompleks itu kan adalah himpunan terbuka yang berwujud lingkaran.

Wujud persekitaran $V_{\frac{1}{3}}(i)$ itu adalah himpunan terbuka berwujud lingkaran dengan titik pusatnya adalah $i$ dan jari-jarinya adalah $\displaystyle \frac{1}{3}$. Grafiknya adalah seperti di bawah ini.

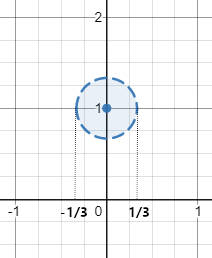
Dari grafik di atas terlihat bahwa titik-titik yang berada di dalam lingkaran biru tidak lain adalah para $z \in \mathbb{C}$ yang memenuhi pertidaksamaan $|z - i| < \frac{1}{3}$.

Perhatikan bahwa lingkaran biru tersebut berada di atas sumbu bagian real. Itu berarti, semua $z \in \mathbb{C}$ yang termuat di lingkaran tersebut memiliki bagian imajiner yang positif. Lebih tepatnya, bagian imajiner yang positif tersebut berada di antara $1 - \frac{1}{3}$ dan $1 + \frac{1}{3}$. Di lain sisi, bagian real berada di antara $-\frac{1}{3}$ dan $\frac{1}{3}$

Dengan kata lain:

 

#Langkah Pembuktian ke-5

Oke, jadi kita sudah membuat $V_{\frac{1}{3}}(i)$. Kemudian, kita ambil sebarang $w \in V_{\frac{1}{3}}(i)$.

Selanjutnya, kita akan menyelidiki $|w + i|$.

Perhatikan bahwa $w = a + bi$ untuk suatu $a,b \in \mathbb{R}$. Lalu, kita akan menjabarkan $|w + i|$ yang hasilnya adalah sebagaimana di bawah ini.

$$\begin{split} |w+i| &= |(a + bi) ~+~ (0 + i)| \\ &= |(a + 0) ~+~ (b + 1)i| \\ &= |a ~+~ (b + 1)i| \\ &= \sqrt{a^2 + (b+1)^2} \\ &= \sqrt{a^2 + b^2 + 2b + 1} \end{split}$$ Dengan demikian, $|w+i| = \sqrt{a^2 + b^2 + 2b + 1}$.  

 

Selanjutnya, kita akan menyelidiki nilai dari $a^2$, $b^2$, dan $2b$. Untuk itu, mari kita mengacu pada Hasil 1 sebagai berikut.

• Berdasarkan Hasil 1, karena $-\frac{1}{3} < a < \frac{1}{3}$, maka $0 \leq a^2 < \frac{1}{9}$.
• Berdasarkan Hasil 1, karena $\frac{2}{3} < b < \frac{4}{3}$, maka $\frac{4}{9} < b^2 < \frac{16}{9}$ dan $\frac{4}{3} < 2b < \frac{8}{3}$.

 

Jika kita mengambil batas bawah dari $a^2$, $b^2$, dan $2b$, maka kita akan mendapatkan hasil berikut.

$$\begin{split} \displaystyle a^2 + b^2 + 2b + 1 &> 0 ~+~ \frac{4}{9} ~+~ \frac{4}{3} ~+~ 1 \\ &~~~=\frac{4+12+9}{9} \\ &~~~=\frac{25}{9} \\ \end{split}$$ Dengan demikian, kita memperoleh $\displaystyle a^2 + b^2 + 2b + 1 ~>~ \frac{25}{9}$.

Karena $\displaystyle \frac{25}{9} > 1$, maka kita akan memperoleh $\displaystyle a^2 + b^2 + 2b + 1 > 1$.

Dengan demikian, $\sqrt{a^2 + b^2 + 2b + 1} ~>~ \sqrt{1}$.

Dengan demikian, $|w+i| > 1$.

Dengan demikian, $\displaystyle \frac{1}{|w+i|} < 1$.

 

#Langkah Pembuktian ke-6: Akhir

Ini adalah bagian akhir pembuktian $\displaystyle \lim_{z \to i}{\frac{z}{z+i}=\frac{1}{2}}$ menggunakan konsep $\epsilon$-$\delta$. Kita akan merangkai segala hal yang sudah kita dapatkan sejauh ini menjadi suatu kesatuan pembuktian.

 

Kita memperoleh sebarang persekitaran dari $\displaystyle \frac{1}{2}$. Persekitaran ini memiliki radius bernilai $\epsilon$. Kita notasikan persekitaran ini sebagai $V_{\epsilon}(\frac{1}{2})$.

Selanjutnya, kita buat persekitaran dari $i$ dengan radius $\frac{1}{3}$. Kita notasikan persekitaran ini sebagai $V_{\frac{1}{3}}(i)$.

Selanjutnya, kita ambil sebarang $w \in V_{\frac{1}{3}}(i)$. Dengan demikian, $w$ akan memenuhi pertidaksamaan $\displaystyle |w - i| < \frac{1}{3}$ dan $\displaystyle \frac{1}{|w+i|} < 1$.

 

Kemudian kita akan menyelidiki apakah $f(w) \in V_{\epsilon}(\frac{1}{2})$ dengan cara membuktikan bahwa $w$ memenuhi pertidaksamaan $\displaystyle \frac{\big|w-i\big|}{2\;\big|w+i\big|} < \epsilon$.

Karena $\displaystyle |w - i| < \frac{1}{3}$ dan $\displaystyle \frac{1}{|w+i|} < 1$, maka:

$\displaystyle \frac{\big|w-i\big|}{2\;\big|w+i\big|} ~~=~~ \frac{1}{2} \cdot |w-i| \cdot \frac{1}{|w+i|} ~~<~~ \frac{1}{2} \cdot \frac{1}{3} \cdot 1 = \frac{1}{6}$

Dengan demikian, jika $w \in V_{\frac{1}{3}}(i)$, maka akan menyebabkan $\displaystyle \frac{\big|w-i\big|}{2\;\big|w+i\big|} < \frac{1}{6}$.

 

Perhatikan!

Persekitaran $V_{\frac{1}{3}}(i)$ sangat bermanfaat untuk $\displaystyle \epsilon \geq \frac{1}{6}$.

Karena untuk setiap $w \in V_{\frac{1}{3}}(i)$ akan mengakibatkan $\displaystyle \frac{\big|w-i\big|}{2\;\big|w+i\big|} < \frac{1}{6} \leq \epsilon$.

 

Akan tetapi, kan nilai $\epsilon > 0$ itu kita dapatkan secara sebarang.

Tidak ada jaminan bahwa nilai $\epsilon > 0$ yang kita dapatkan itu selalu $\displaystyle \geq \frac{1}{6}$ kan? 

Bagaimana jika kita mendapatkan nilai $\displaystyle \epsilon < \frac{1}{6}$?

 

Perhatikan!

Jika $\displaystyle 0 < \epsilon < \frac{1}{6}$, maka akan berlaku $\displaystyle 0 < 2\epsilon < \frac{1}{3}$. Nilai $2\epsilon$ akan lebih kecil dari $\displaystyle \frac{1}{3}$.

Berdasarkan Sifat 1, dengan titik pusat yang sama, maka persekitaran dengan radius $2\epsilon$ akan berada di dalam persekitaran dengan radius $\displaystyle \frac{1}{3}$.

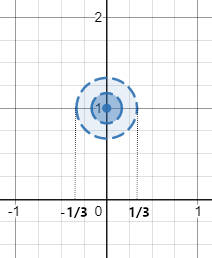
Dengan demikian, jika $w \in V_{2\epsilon}(i)$, maka $w \in V_{\frac{1}{3}}(i)$.

Dengan demikian, jika $w$ memenuhi pertidaksamaan $|w - i| < 2\epsilon$, maka $w$ juga memenuhi pertidaksamaan $\displaystyle |w - i| < \frac{1}{3}$.

Dengan demikian, jika $w$ memenuhi pertidaksamaan $|w - i| < 2\epsilon$, maka $\displaystyle \frac{1}{|w+i|} < 1$.

 

Karena $|w - i| < 2\epsilon$ dan $\displaystyle \frac{1}{|w+i|} < 1$, maka:

$\displaystyle \frac{\big|w-i\big|}{2\;\big|w+i\big|} ~~=~~ \frac{1}{2} \cdot |w-i| \cdot \frac{1}{|w+i|} ~~<~~ \frac{1}{2} \cdot 2\epsilon \cdot 1 = \frac{2\epsilon}{2} = \epsilon$

Dengan demikian, jika $w \in V_{2\epsilon}(i)$, maka akan menyebabkan $\displaystyle \frac{\big|w-i\big|}{2\;\big|w+i\big|} < \epsilon$.

Eh! Ingat ya! Ini khusus untuk kasus $\displaystyle \epsilon < \frac{1}{6}$ lho!

 

Dari Hasil 3 dan Hasil 4 di atas, kita memperoleh 2 pilihan $\delta$, yaitu $\displaystyle \delta_1 = \frac{1}{3}$ dan $\displaystyle \delta_2 = 2\epsilon$. Mana $\delta$ yang kita pilih bergantung dari nilai $\epsilon$ yang kita peroleh.

Supaya lebih mudah, kita dapat menentukan $\delta$ sebagai yang terkecil di antara $\displaystyle \delta_1 = \frac{1}{3}$ dan $\displaystyle \delta_2 = 2\epsilon$.

 

Kenapa dipilih yang terkecil?

 

Karena kita ingin memastikan bahwa semua $w \in \mathbb{C}$ yang berada di dalam persekitaran $\delta$ tersebut memenuhi $f(w) \in V_{\epsilon}(\frac{1}{2})$. Lagipula, jika titik pusatnya sama, maka persekitaran dengan radius terkecil akan termuat di dalam persekitaran dengan radius terbesar. Hal tersebut berarti, sifat-sifat yang berlaku di dalam persekitaran dengan radius terbesar juga berlaku di dalam persekitaran dengan radius terkecil.

 

#Kesimpulan

Jadi, berdasarkan uraian panjang di atas, telah terbukti benar menggunakan konsep $\epsilon$-$\delta$ bahwa $\displaystyle \lim_{z \to i}{\frac{z}{z+i}=\frac{1}{2}}$.

Karena untuk sebarang $V_{\epsilon}$, kita dapat membentuk persekitaran $V_{\delta}(i)(\frac{1}{2})$ dengan nilai $\delta$ sebagai yang terkecil di antara $\frac{1}{3}$ dan $2 \epsilon$, sedemikian sehingga untuk setiap $z \in V_{\delta}(i)$ akan berakibat $\displaystyle \Bigg|\frac{z}{z+i} - \frac{1}{2}\Bigg| < \epsilon$.

 

Oh, ya!

Sebagai latihan, kalian bisa memilih nilai $\delta$ pada Langkah Pembuktian ke-3 sebagai $\displaystyle \frac{1}{\text{tanggal lahir ibumu}}$ dan lihat nilai apa saja yang pada akhirnya dapat dipilih sebagai $\delta$.

 

"...dore dake kimi wo aishitara
kono omoi todoku no darou
yume no naka de wa tashikani
ieta hazu na noni..."