Cara Menentukan Komposisi Fungsi Piecewise dan Domainnya #1

Dalam matematika, jika kita menyinggung topik tentang fungsi, pastilah komposisi fungsi tidak akan terlupa untuk dibahas.  

Komposisi fungsi adalah topik yang umum dipelajari pada mata kuliah Kalkulus I. Selain di jenjang kuliah, umumnya topik komposisi fungsi juga dipelajari pada kelas 10 SMA.

Hanya saja, jika dibandingkan dengan jenjang SMA, topik komposisi fungsi pada jenjang perkuliahan terasa lebih sulit. Bisa jadi, hal tersebut dikarenakan topik komposisi fungsi pada jenjang perkuliahan sering melibatkan fungsi piecewise (piecewise function). Di bawah ini adalah contoh fungsi piecewise.

$f(x) = \begin{cases} x^2 & \text{,untuk } x\leq 0 \\ \frac{100-x}{100} & \text{,untuk } 0 < x < 100 \\ 0 & \text{,untuk } x \geq 100 \end{cases}$

Sebagaimana yang terlihat pada contoh di atas, bentuk fungsi piecewise rasanya tidak terlalu sulit untuk dipahami. Mungkin karena fungsi piecewise amat jarang disinggung pada matematika SMA, akibatnya banyak mahasiswa baru yang kesulitan mendalami topik komposisi fungsi pada mata kuliah Kalkulus I.

 

Nah, pada tulisan ini, kita akan mencoba untuk menyelesaikan soal komposisi fungsi yang melibatkan fungsi piecewise.

Semoga bisa memberi sedikit pencerahan bagi yang baru mempelajari topik komposisi fungsi di mata kuliah Kalkulus I.

 

Soal

Tentukan $g \circ f$ beserta domainnya, jika diketahui

$\displaystyle f(x) = \frac{x-3}{x+2}$ dan 

$ g(x) = \begin{cases} \sqrt{x} & \text{,untuk } x\geq 0 \\ & \\ \displaystyle \frac{1-x}{x} & \text{,untuk } x < 0 \end{cases}$.

 

Pembahasan

#Langkah 1.
Pahami dulu apa itu $g \circ f$!

Komposisi fungsi $g \circ f$ itu artinya adalah mengevaluasi hasil dari fungsi $f$ terlebih dahulu. Baru setelah itu hasil dari fungsi $f$ dievaluasi terhadap fungsi $g$. 

Urutan langkahnya:

1. Ambil $x$ elemen $\text{Domain}(f)$.
2. Selidiki nilai $\alpha = f(x)$.
3. Selidiki nilai $g(\alpha)$.

 

#Langkah 2.
Selidiki dulu $\text{Domain}(f)$!

Diketahui bahwa $\displaystyle f(x) = \frac{x-3}{x+2}$.

Perhatikan bahwa fungsi $f$ memiliki penyebut $x+2$. Kita tahu bahwa jika $x=-2$, maka $x + 2 = -2 + 2 = 0$. Akibatnya fungsi $f$ tidak terdefinisi di $x = -2$.

Selain di $x=-2$, fungsi $f$ terdefinisi dengan baik.

Jadi $\text{Domain}(f) = \mathbb{R} - \{-2\}$.

 

#Langkah 3.
Selidiki $\text{Range}(f)$.

$\text{Range}(f)$ itu paling enak dibaca dengan menggunakan grafik. Untuk membuat grafik tersebut kita terlebih dahulu harus menyelidiki sejumlah hal, seperti:

##1. Apakah fungsi $f$ memotong sumbu X?

Ingat! Jika fungsi $f$ memotong sumbu X, maka terdapat $\alpha \in \text{Domain}(f)$ sedemikian sehingga $f(\alpha) = 0$. 

Pertanyaannya, apakah $\alpha$ yang dimaksud itu ada?

 

Jika $\alpha$ yang dimaksud itu ada, maka $\displaystyle 0 = f(\alpha) = \frac{\alpha-3}{\alpha+2}$.

Perhatikan bahwa $f(\alpha) = 0 \iff \alpha-3 = 0 \iff \alpha = 3$.

Karena $3 \in \text{Domain}(f) = \mathbb{R} - \{-2\}$, maka dapat disimpulkan bahwa fungsi $f$ memotong sumbu X di titik $(3, 0)$.  

 

##2. Apakah fungsi $f$ memotong sumbu Y?

Ingat! Fungsi $f$ memotong sumbu Y jika dan hanya jika $x = 0$. Karena $0 \in \text{Domain}(f) = \mathbb{R} - \{-2\}$, maka dapat disimpulkan bahwa fungsi $f$ memotong sumbu Y.

Pertanyaannya, fungsi $f$ memotong sumbu Y di titik apa?

 

Ya, tinggal dihitung saja nilai dari $\displaystyle f(0) = \frac{0-3}{0+2} = - \frac{3}{2}$.

Jadi, fungsi $f$ memotong sumbu Y di titik $\displaystyle(0, - \frac{3}{2})$.

 

##3. Apakah karakteristik fungsi $f$?

Karakteristik suatu fungsi digunakan untuk mengetahui wujud dari grafik fungsi, apakah linear, kurva, atau hiperbola.

Kembali pada fungsi $\displaystyle f(x) = \frac{x-3}{x+2}$.

Perhatikan bahwa fungsi $f$ dapat diubah bentuknya menjadi seperti ini.

$\displaystyle f(x) = \frac{x-3}{x+2} = \frac{x+2 - 5}{x+2} = \frac{x+2}{x+2} - \frac{5}{x+2} = 1 - 5\left(\frac{1}{x+2}\right)$.

Dari penjabaran di atas kita akan memperoleh:

$\displaystyle f(x) = 1 - 5\left(\frac{1}{x+2}\right)$.

Dari sini terlihat bahwa untuk apapun $x \in \text{Domain}(f) = \mathbb{R} - \{-2\}$, nilai $f(x) = 1$ TIDAK AKAN TERJADI.

Kenapa?

Itu karena $\displaystyle \frac{1}{x+2}$ tidak akan pernah $=0$!

 

Kita tahu bahwa $\displaystyle \frac{1}{x+2}$ tidak terdefinisi untuk $x = -2$.

Mari kita selidiki lebih lanjut dengan mencari tahu seperti apakah nilai $\displaystyle \frac{1}{x+2}$ untuk $x$ yang mendekati $-2$, baik dari kanan maupun dari kiri.

 

Kita selidiki untuk $x$ yang mendekati $-2$ dari arah kanan. Misalkan saja $x = -1,999999$.

Perhatikan bahwa:

$\displaystyle \frac{1}{x+2} = \frac{1}{-1,999999 + 2} = \frac{1}{0,000001} = 1.000.000$.

Dari sini dapat disimpulkan, untuk $x$ yang mendekati $-2$ dari arah kanan, maka $\displaystyle \frac{1}{x+2}$ akan menuju $\infty$.

Akibatnya, untuk $x$ yang mendekati $-2$ dari arah kanan, $\displaystyle f(x) = 1 - 5\left(\frac{1}{x+2}\right)$ akan menuju ke $-\infty$.

 

Dengan cara yang serupa, kita dapat menyelidiki untuk $x$ yang mendekati $-2$ dari arah kiri.

Untuk $x$ yang mendekati $-2$ dari arah kiri, $\displaystyle f(x) = 1 - 5\left(\frac{1}{x+2}\right)$ akan menuju ke $+\infty$.

 

Berikut adalah grafik fungsi $f$.

 

 

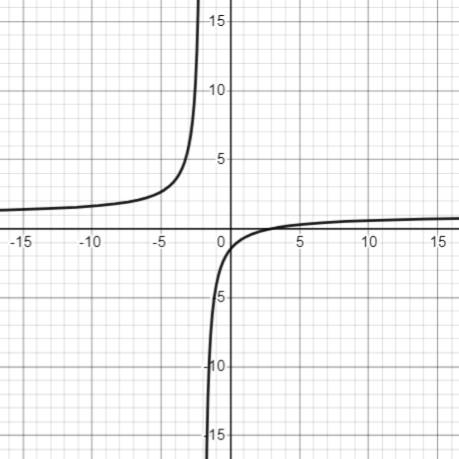
Dari grafik di atas kita dapat menyimpulkan bahwa $\text{Range}(f) = (-\infty, 1) \cup (1, \infty)$, dengan 

• $(-\infty, 1) = \{ x < 1 ~|~ x \in \mathbb{R} \}$, dan
• $(1, \infty) = \{ x > 1 ~|~ x \in \mathbb{R} \}$.

 

#Langkah 4.
Selidiki $\text{Domain}(g)$!

Diketahui 

$ g(x) = \begin{cases} \sqrt{x} & \text{,untuk } x\geq 0 \\ & \\ \displaystyle \frac{1-x}{x} & \text{,untuk } x < 0 \end{cases}$.

 

Fungsi $g$ tersebut merupakan fungsi piecewise. Untuk mempermudah penyebutan, fungsi piecewise tersebut kita pecah sebagai fungsi $g_1$ dan $g_2$ sebagai berikut.

• $g_1(x) = \sqrt{x}$, dan
• $g_2(x) = \displaystyle \frac{1-x}{x}$.

 

Sehingga dengan demikian

$ g(x) = \begin{cases} g_1(x) & \text{,untuk } x\geq 0 \\ & \\ g_2(x) & \text{,untuk } x < 0 \end{cases}$.

 

Selanjutnya, kita akan menyelidiki fungsi $g_1$ dan $g_2$, seperti apakah sebetulnya mereka.

 

##1. Selidik fungsi $g_1$.

Diketahui $g_1(x) = \sqrt{x}$ dengan domainnya adalah $x\geq 0$.

Sesuai definisi di atas, fungsi $g_1$ terdefinisi dengan baik. Untuk setiap $x\geq 0$, nilai $g_1(x)$ akan selalu $\geq 0$.

 

##2. Selidik fungsi $g_2$.

Diketahui $g_2(x) = \displaystyle \frac{1-x}{x} = \frac{1}{x} - 1$ dengan domainnya adalah $x < 0$.

Sesuai definisi di atas, fungsi $g_2$ terdefinisi dengan baik. Untuk setiap $x < 0$, nilai $g_2(x)$ akan selalu $< 0$.

 

Dari hasil penyelidikan di atas, diketahui bahwa fungsi $g_1$ dan $g_2$ terdefinisi dengan baik.

Jadi, dapat disimpulkan bahwa $\text{Domain}(g) = \mathbb{R}$.

 

#Langkah 5.
Selidiki apakah $\text{Range}(f) \subseteq \text{Domain}(g)$.

Dari Langkah 3 di atas, kita mengetahui bahwa $\text{Range}(f) = (-\infty, 1) \cup (1, \infty)$.

Dari Langkah 4 di atas, kita mengetahui bahwa $\text{Domain}(g) = \mathbb{R}$.

 

Perhatikan bahwa $\text{Range}(f) = (-\infty, 1) \cup (1, \infty) = \mathbb{R} - \{1\}$.

Jelas bahwa $\mathbb{R} - \{1\} \subset \mathbb{R}$.

 

Dengan demikian berlaku $\text{Range}(f) \subset \text{Domain}(g)$.

Dengan kata lain komposisi fungsi $g \circ f$ dapat dilakukan.

 

#Langkah 6.
Konstruksi $\text{Domain}(g \circ f)$.

Nah, bagian ini yang umumnya paling sering membuat bingung mahasiswa yang baru mempelajari Kalkulus I. 

Mari kita kerjakan secara pelan-pelan dan hati-hati supaya tidak salah. :D

 

##Langkah 1

Karena yang "misi" kita adalah mengkonstruksi $\text{Domain}(g \circ f)$, maka pertama-tama kita harus mengamati fungsi $g$.

Sebaliknya, jika "misi" kita adalah mengkonstruksi $\text{Domain}(f \circ g)$, maka pertama-tama kita harus mengamati fungsi $f$.

 

Kembali ke "misi" utama kita sesuai pada soal.

Kita akan mengkonstruksi $\text{Domain}(g \circ f)$. Oleh sebab itu, pertama-tama kita harus mengamati fungsi $g$.

 

Ini adalah fungsi $g$ yang dimaksud.

$g(x) = \begin{cases} g_1(x) = \sqrt{x} & \text{,untuk } x\geq 0 \\ & \\ \displaystyle g_2(x) = \frac{1-x}{x} & \text{,untuk } x < 0 \end{cases}$.

 

##Langkah 2

Selanjutnya, ajukan pertanyaan berikut.

Apakah fungsi $g$ adalah fungsi piecewise?

 

Jawabannya jelas adalah YA.

Fungsi $g$ merupakan fungsi piecewise dengan 2 subfungsi, yaitu $g_1$ dan $g_2$.

 

Selanjutnya, kita akan menyelidiki domain-domain subfungsi dari fungsi $g$, yaitu $g_1$ dan $g_2$.

 

##Langkah 3

Kita mulai dengan menyelidiki domain dari fungsi $g_1$.

$g_1(x) = \sqrt{x} ~\text{,  untuk } x\geq 0$

 

Ajukan pertanyaan ini.

Untuk $\alpha \in \text{Domain}(f)$ apa sajakah yang menyebabkan $f(\alpha) \geq 0$?

 

Perhatikan bahwa syarat kondisi $f(\alpha) \geq 0$ adalah sesuai dengan syarat domain $g_1$ yaitu $x \geq 0$. 

 

Kita lihat lagi grafik fungsi $f$ berikut. Perhatikan bagian kurva yang berwarna merah.

 

 

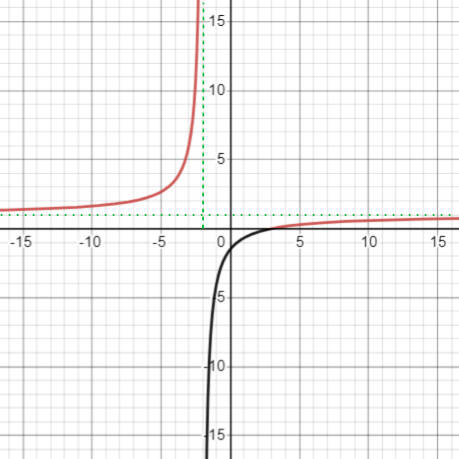
Dari bagian yang berwarna merah di atas terlihat bahwa jika $\alpha$ berada di interval $(-\infty, -2)$ dan $[3, \infty)$ akan menyebabkan $f(\alpha) \geq 0$.  

 

Karena $\displaystyle f(x) = \frac{x-3}{x+2}$ bukan fungsi piecewise, maka dengan demikian,

$\displaystyle (g_1 \circ f)(x) = g_1(f(x)) = \sqrt{\frac{x-3}{x+2}}$ berlaku dan terdefinisi dengan baik jika $x$ berada di interval $(-\infty, -2)$ dan $[3, \infty)$.  

 

##Langkah 4

Kita lanjut dengan menyelidiki domain dari fungsi $g_2$.

$\displaystyle g_2(x) = \frac{1-x}{x} = \frac{1}{x} - 1 ~\text{,   untuk } x < 0$

 

Ajukan pertanyaan ini.

Untuk $\alpha \in \text{Domain}(f)$ apa sajakah yang menyebabkan $f(\alpha) < 0$?

 

Perhatikan bahwa syarat kondisi $f(\alpha) < 0$ adalah sesuai dengan syarat domain $g_2$ yaitu $x < 0$. 

 

Kita lihat lagi grafik fungsi $f$ ini. Perhatikan bagian kurva yang berwarna ungu.

 

 

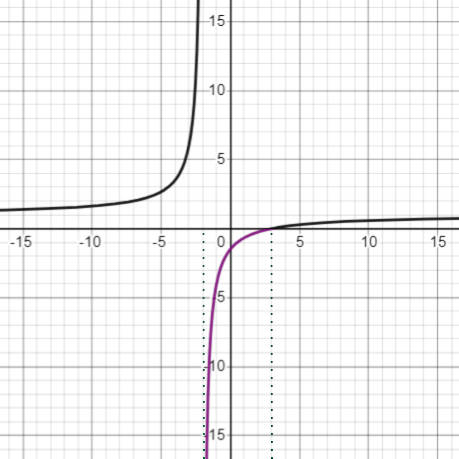
Dari bagian yang berwarna ungu di atas terlihat bahwa jika $\alpha$ berada di interval $(-2, 3)$ akan menyebabkan $f(\alpha) < 0$.

 

Karena $\displaystyle f(x) = \frac{x-3}{x+2}$ bukan fungsi piecewise, maka dengan demikian,

$\displaystyle (g_2 \circ f)(x) = g_2(f(x)) = \frac{1}{\left(\frac{x-3}{x+2}\right)} - 1 = \frac{5}{x-3}$ berlaku dan terdefinisi dengan baik jika $x$ berada di interval $(-2, 3)$.  

 

#Langkah 7.
Penyatuan Hasil.

Dari Langkah 6 di atas kita mendapatkan hasil berikut.

• $\displaystyle (g_1 \circ f)(x) = g_1(f(x)) = \sqrt{\frac{x-3}{x+2}}$ berlaku dan terdefinisi dengan baik jika $x$ berada di interval $(-\infty, -2)$ dan $[3, \infty)$.
• $\displaystyle (g_2 \circ f)(x) = g_2(f(x)) = \frac{1}{\left(\frac{x-3}{x+2}\right)} - 1 = \frac{5}{x-3}$ berlaku dan terdefinisi dengan baik jika $x$ berada di interval $(-2, 3)$.

 

Dari hasil di atas, $g \circ f$ beserta domainnya dapat dibentuk sebagaimana berikut.

$(g\circ f)(x) = \begin{cases} \displaystyle \sqrt{\frac{x-3}{x+2}} & \text{,untuk } x \in (-\infty, -2) ~\text{ alias } x < -2 \\ \text{tidak terdefinisi} & \text{,untuk } x = -2  \\ & \\ \displaystyle \frac{5}{x-3} & \text{,untuk } x \in (-2,3) ~\text{ alias } -2 < x < 3 \\ & \\ \displaystyle \sqrt{\frac{x-3}{x+2}} & \text{,untuk } x \in [3, \infty) ~\text{ alias } x \geq 3 \end{cases}$